<[induced-electromotive-force-at-any-instant丨analyse丨]>
202502281652L₂是我的身高,L₁是我的双臂之间的“距离”!
任意时刻线圈感应电动势的表达式
1. 小胖子的问题
1.1 中性面与与中性面垂直的平面
- 小胖子说:“我已经知道了中心面的感应电动势是零,与中心面垂直的平面感应电动势是。那如果是任意时刻感应电动势,又怎么表示呢?今天咱们就来研究这个问题。”
1.2 交流发电机的正视图分析
-
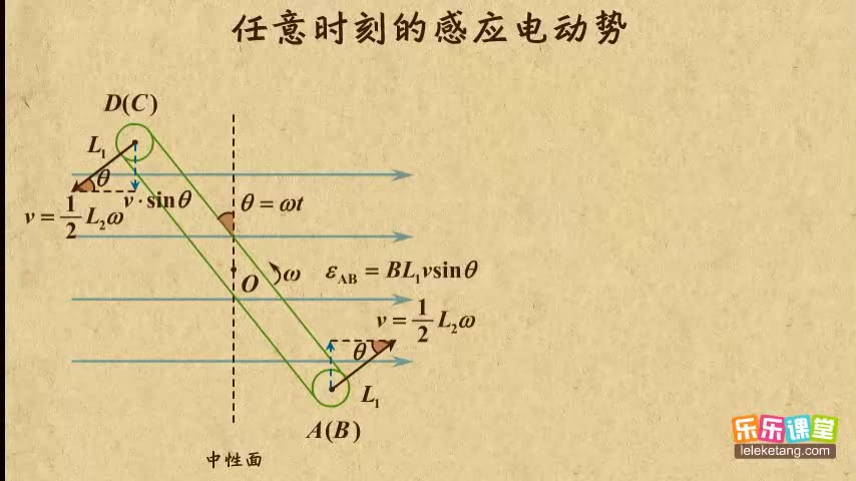
来看交流发电机的正视图,咱只能看到AD边,长度为,AB边和CD边看起来是一个点,长度为。转轴在AD的中央,假设匀速转动的角速度为。
-
那么如果从中性面开始计时,经过时间,线圈与中心面的夹角,并且任意时刻AB边的速度都是,CD边也是。
-
但是只有垂直于磁场的速度分量才能产生感应电动势,因此其中一条边产生的电动势大小为。把和代入,可以得到一条边的电动势是这样的。
-
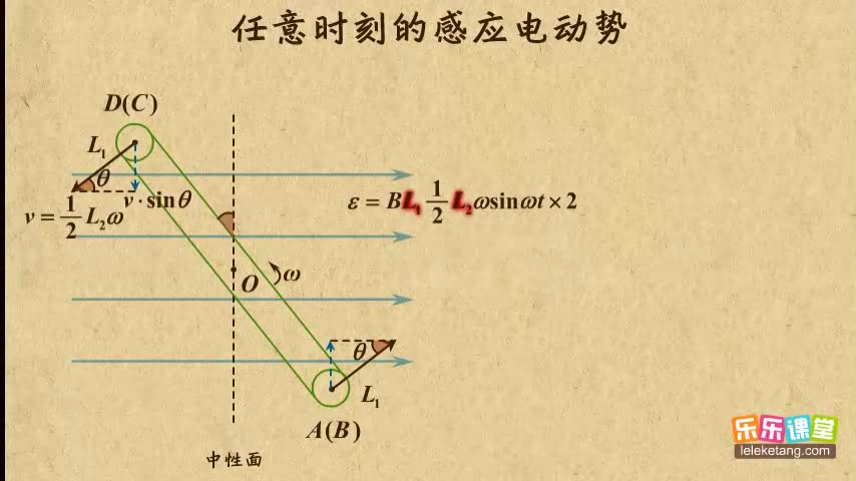
而计算总电动势时,又有两条边在切割磁感线,所以总电动势要乘以二。就是线圈的面积,咱们用来表示,化简一下就是这样。
-
刚才分析的是单匝线圈的情况,如果线圈不是单匝而是匝,那么总电动势要再乘以。这里的是电动势的最大值,再把它记为,那么总电动势就是它乘上,这就是线圈从中心面开始转动,任意时刻感应电动势的表达式。
1.3 初始位置对电动势的影响
-
这里的是线圈跟中心面的夹角,那么如果线圈是从与中心面垂直的平面开始转动呢?很简单,这相当于变成了线圈跟这个平面的夹角,那么此时线圈跟中心面的夹角就是。
-
把这个夹角代入刚才的表达式,化简后就是这样,你看只是正弦变成了余弦而已,它俩的区别在于线圈是从中性面还是从与中性面垂直的平面开始转动。
-
这里要注意一点,虽然刚才的推导是对转轴在中央的矩形线圈,但其实无论线圈的形状和转轴的位置如何,这几个结论仍然是成立的。
2. 小胖子的进一步提问
2.1 如果初始位置既不是中心面也不是与中心面垂直的平面
- 求知欲很强的小胖子还是不满足,他又问:“那如果线圈出发的位置既不是中心面,也不是与中心面垂直的平面,电动势又该怎么算呢?”
2.2 解决方法
-
这个问题也不难,假设线圈在初始时刻与中心面的夹角为,那么经过时间,线圈与中心面的夹角就比原来多个,所以电动势的公式里也要加一个。
-
同样的,如果线圈在初始时刻跟与中心面垂直的平面夹角为,那么电动势的表达式就是这个样子。
3. 总结
-
总结一下,线圈转动时感应电动势的最大值是,如果从中心面开始转动,电动势就是它乘上;如果从与中心面垂直的平面开始转动,电动势就是它乘;而对于从任意时刻开始转动的情况,只要把初始夹角填上就行了。
-
只需要注意这里的表示初始位置与中心面的夹角,而这里的表示初始位置与跟中心面垂直的平面的夹角,千万不要记混了。
-
好了,知识就先说这么多,快去刷几道题吧。
The answer. #/Q